75 horas pedagógicas
Unidad 1: Números de más de 6 cifras. Cálculos con las cuatro operaciones y el uso de paréntesis. Reglas de secuencias numéricas. Ecuaciones.
Números naturales de más de seis cifras. Cálculos con las cuatro operaciones y el uso de paréntesis. Ecuaciones e inecuaciones de un paso. Secuencias numéricas.
Propósito
Se espera que, en esta unidad, los estudiantes profundicen el trabajo con números naturales, ampliando el ámbito numérico a números de hasta más de 6 cifras, representando, describiendo, comparando, aproximando y estimando estos números, demostrando la comprensión de multiplicaciones y divisiones, y aplicando estrategias de cálculo mental y escrito en el contexto de la resolución de problemas en contextos diversos. A su vez, se espera que, en el ámbito del eje de patrones y relaciones, los alumnos demuestren comprensión con respecto a que una secuencia admite más de un patrón, creen ecuaciones de primer grado con una incógnita y resuelvan estas ecuaciones en el contexto de la resolución de problemas. El foco de la unidad está puesto en la resolución de problemas y, en este sentido, los elementos que aportan la operatoria con números naturales y las ecuaciones y su trabajo en conjunto a esta resolución.
Conocimientos previos
Conteo, lectura y escritura de números naturales de hasta 5 cifras. Representar y describir números de hasta 5 cifras. Comparar y ordenar números de hasta 5 cifras. Estimar productos de 3 dígitos por 2 dígitos y cocientes de hasta 4 dígitos por 1 dígito. Resolver problemas, aplicando las cuatro propiedades en el ámbito numérico hasta 100 000. Creación y resolución de ecuaciones en el ámbito hasta el 1 000.
Palabras claves
Tabla de valor posicional. Pictórico. Simbólico. Redondear. Aproximar. Comparar. Ordenar. Estimar. Estrategias de cálculo. Patrones. Producto. Cociente. Resto. Decena y centena de mil. Resolución de ecuaciones. Creación de ecuaciones. Incógnita. Problemas rutinarios. Problemas no rutinarios.
Objetivos de la unidad
Representar y describir números naturales de hasta más de 6 dígitos y menores que 1 000 millones:
- identificando el valor posicional de los dígitos
- componiendo y descomponiendo números naturales en forma estándar y expandida aproximando cantidades
- comparando y ordenando números naturales en este ámbito numérico
- dando ejemplos de estos números naturales en contextos reales.
Indicadores
Indicadores Unidad 1
- Describen el significado de cada dígito de un número determinado.
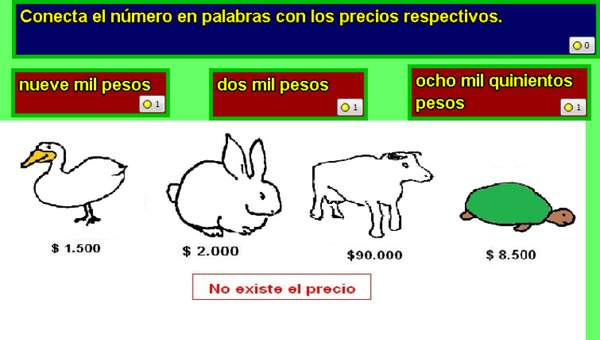
- Dan ejemplos de números grandes utilizados en medios impresos o electrónicos.
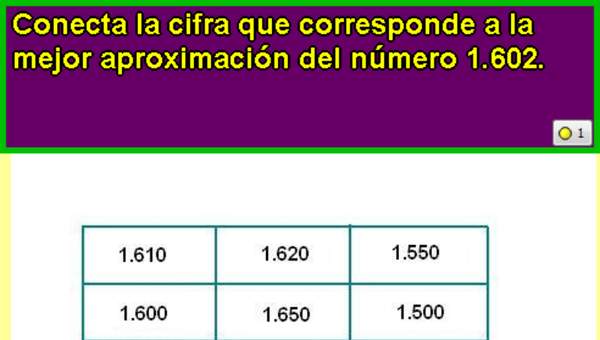
- Aproximan números, usando el valor posicional. Por ejemplo: aproximan 43 950 a la unidad de mil más cercana.
- Expresan un número dado en notación expandida. Por ejemplo: expresan 53 657 en la forma:
- 5 X 10 000 + 3 x 1 000 + 6 x 100 + 5 x 10 + 7.
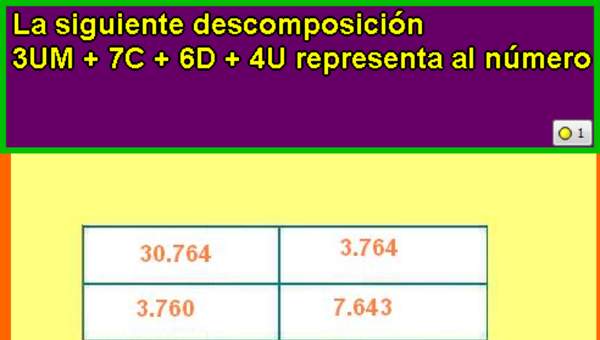
- Escriben en notación estándar el numeral representado en notación expandida.
- Explican y muestran el significado de las cifras en números cuyas cifras se repiten. Por ejemplo, en 555 555, explican que el primer número representa 5 centenas de mil, que el segundo número representa 5 decenas de mil, etc.
- Explican, por medio de ejemplos, estrategias para comparar números.
- Ordenan números de manera creciente y decreciente.
- Explican el orden de números, empleando el valor posicional.
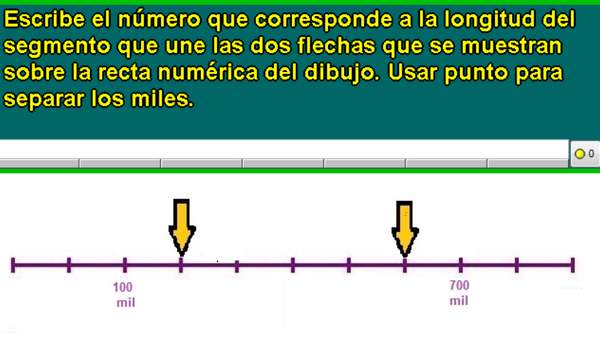
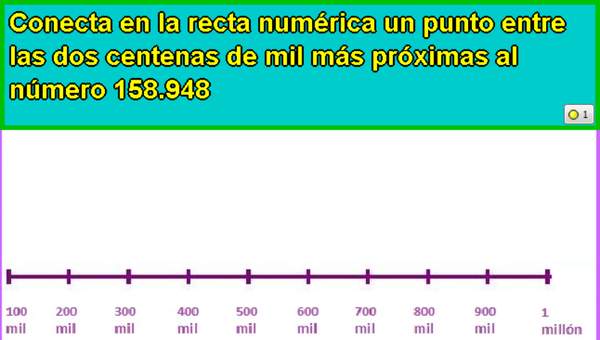
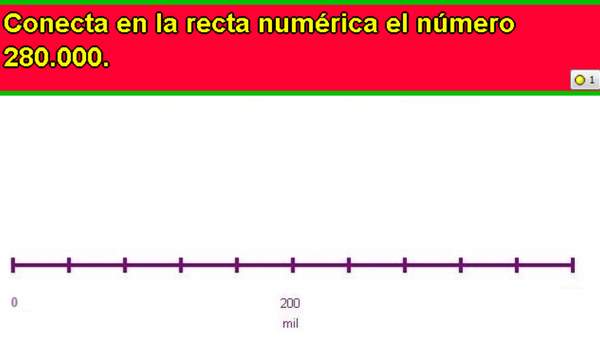
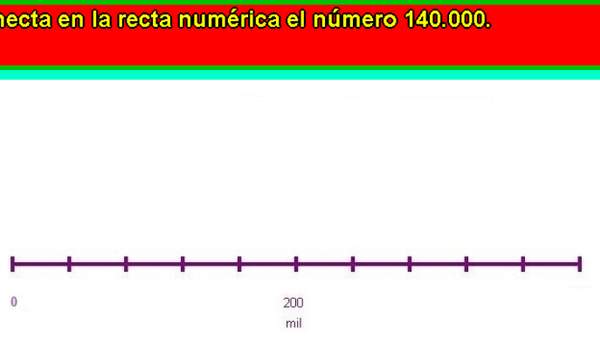
- Dividen en partes iguales tramos de la recta numérica. Por ejemplo: entre 100 000 y 1 000 000.
- Identifican el primer, segundo, tercer término en secuencias ordenadas.
- Intercalan números entre números en la recta numérica. Por ejemplo: intercalan dos números entre 10 000 y 10 004
Aplicar estrategias de cálculo mental para la multiplicación:
- anexar ceros cuando se multiplica por un múltiplo de 10
- doblar y dividir por 2 en forma repetida
- usando las propiedades conmutativa, asociativa y distributiva.
Indicadores
Indicadores Unidad 1
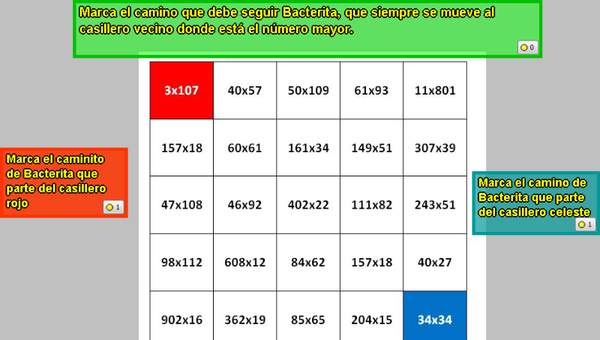
- Determinan productos cuando uno de los factores es múltiplo de 10, 100 o 1 000.
- Calculan multiplicaciones, aplicando mitades y dobles.
- Por ejemplo: 34 · 5 = 17 · 10.
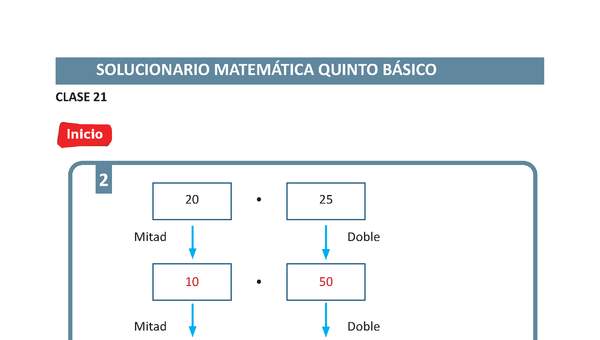
- Calculan multiplicaciones, aplicando repetidamente dobles y mitades.
- Por ejemplo: 12 · 25 = 6 · 50 = 3 · 100.
- Aplican la propiedad distributiva en multiplicaciones, descomponiendo en múltiplos de 10.
- Por ejemplo: 102 · 4 = (100 + 2) · 4 = 100 · 4 + 2 · 4.
- Doblan multiplicaciones dadas para realizar multiplicaciones.
- Por ejemplo: para calcular 12 x 3, piensan en 6x3 y la doblan.
- Usan las propiedades conmutativa y asociativa para multiplicar números.
- Por ejemplo: 25 · (3 · 4) = 25 · (4 · 3) = (25 · 4) · 3 = 100 · 3 = 300.
Demostrar que comprenden la multiplicación de números naturales de dos dígitos por números naturales de dos dígitos:
- estimando productos
- aplicando estrategias de cálculo mental
- resolviendo problemas rutinarios y no rutinarios aplicando el algoritmo.
Indicadores
Indicadores Unidad 1
- Aplican redondeo para estimar productos y emplean la calculadora para comprobar la estimación dada.
- Por ejemplo, 42 · 58 40 · 60 = 2 400, y usan la calculadora para comprobar este resultado.
- Aplican la propiedad distributiva para multiplicar números.
- Por ejemplo: 12 · 50 = (10 + 2) · 50 = 10 · 50 + 2 · 50 = 500 + 100 = 600.
- Usan propiedades del cálculo mental, como las propiedades conmutativa y asociativa, para multiplicar números.
- Por ejemplo: 25 · 68 = 25 · (17 · 4) = 25 · (4 · 17) = (25 · 4) · 17 = 100 · 17 = 1700.
- Muestran los pasos que se debe dar para multiplicar números de dos dígitos por 11, 12, … 19, usando bloques de base diez, y registran el proceso simbólicamente.
- Resuelven multiplicaciones en el contexto de problemas rutinarios y no rutinarios, usando el algoritmo de la multiplicación.
Demostrar que comprenden la división con dividendos de tres dígitos y divisores de un dígito:
- interpretando el resto
- resolviendo problemas rutinarios y no rutinarios que impliquen divisiones.
Indicadores
Indicadores Unidad 1
- Modelan la división como el proceso de reparto equitativo, usando bloques de base diez, y registran los resultados de manera simbólica.
- Explican el resto de una división en términos del contexto.
- Ignoran el resto de divisiones en el contexto de situaciones.
Por ejemplo: determinan que 5 equipos de 4 personas cada uno se pueden formar con 22 personas. - Redondean cocientes.
- Expresan restos como fracciones.
- Expresan restos como decimales.
- Resuelven un problema no rutinario de división en contexto, usando el algoritmo y registrando el proceso.
Indicadores
Indicadores Unidad 1
- Realizan operaciones combinadas de sumas y restas.
- Realizan operaciones combinadas de sumas y restas que involucran paréntesis.
- Calculan expresiones desconocidas en igualdades en que intervienen sumas y restas.
- Resuelven sumas y/o restas de multiplicaciones y/o divisiones.
- Aplican reglas de paréntesis en la operatoria con expresiones numéricas.
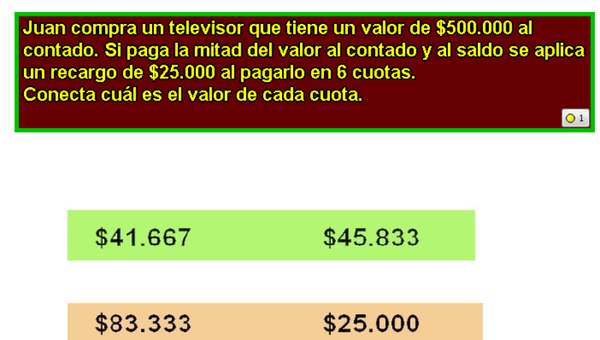
Resolver problemas rutinarios y no rutinarios que involucren las cuatro operaciones y combinaciones de ellas:
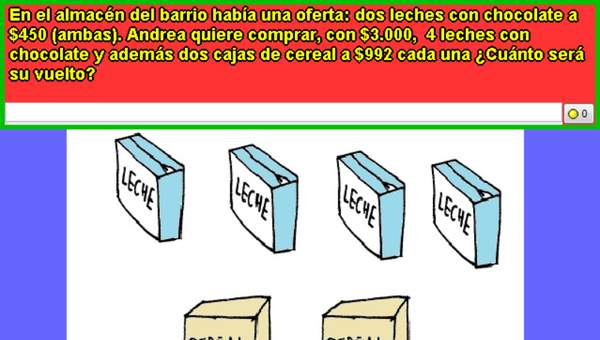
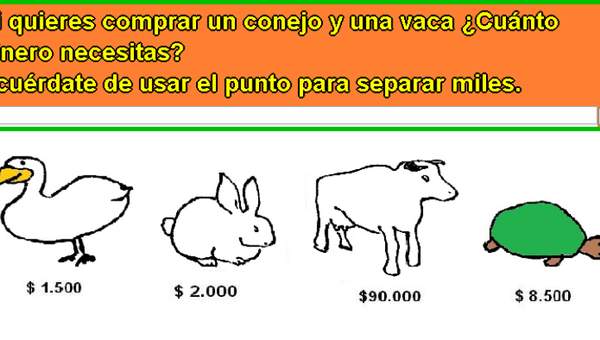
- que incluyan situaciones con dinero
- usando la calculadora y el computador en ámbitos numéricos superiores al 10 000.
Indicadores
Indicadores Unidad 1
- Seleccionan y usan una estrategia para estimar la solución de un problema dado.
- Demuestran que la solución aproximada a un problema no rutinario dado, no requiere de una respuesta exacta.
- Determinan respuestas aproximadas.
- Estiman la solución de un problema dado y lo resuelven.
- Resuelven problemas matemáticos relativos a cálculos de números, usando la calculadora.
- Identifican qué operación es necesaria para resolver un problema dado y lo resuelven.
- Determinan lo razonable de una respuesta a un problema no rutinario.
- Evalúan la solución de un problema en su enunciado.
- Explican la estrategia utilizada para resolver un problema.
Indicadores
Indicadores Unidad 1
- Extienden un patrón numérico con y sin materiales concretos, y explican cómo cada elemento difiere de los anteriores.
- Muestran que una sucesión dada puede tener más de un patrón que la genere. Por ejemplo: la sucesión 2, 4, 6, 8, …puede tener como patrón los números pares consecutivos, o podría ser continuada como 2, 4, 6, 8, 1, 3, 5, 7,… y en este caso podría tener un patrón de cuatro números pares consecutivos y cuatro números impares consecutivos.
- Dan ejemplos de distintos patrones para una sucesión dada y explican la regla de cada uno de ellos.
- Dan una regla para un patrón en una sucesión y completan los elementos que siguen en ella, usando esa regla.
- Describen, oralmente o de manera escrita, un patrón dado, usando lenguaje matemático, como uno más, uno menos, cinco más.
- Describen relaciones en una tabla o un gráfico de manera verbal.
Indicadores
Indicadores Unidad 1
- Expresan un problema mediante una ecuación donde la incógnita está representada por una letra.
- Crean un problema para una ecuación dada.
- Obtienen ecuaciones de situaciones imaginadas sin resolver la ecuación.
- Resuelven una ecuación simple de primer grado con una incógnita que involucre adiciones y sustracciones.
- Evalúan la solución obtenida de un problema en términos del enunciado del problema.
- Explican estrategias para resolver problemas, utilizando ecuaciones.
Comunicar de manera escrita y verbal razonamientos matemáticos:
- describiendo los procedimientos utilizados
- usando los términos matemáticos pertinentes.
Modelar matemáticamente situaciones cotidianas:
- organizando datos
- identificando patrones o regularidades
- usando simbología matemática para expresarlas.
Recursos de la unidad
Clase Aula virtual
Evaluación de las clases
Material para docentes
Plan de lecciones CODE
Plan de trabajo
Solucionario de las clases
Actividades evaluativas
Actividades complementarias
Actividades sugeridas
Actividad evaluación
Libros de actividades
Imágenes
Interactivos
Presentaciones
Videos
Lecturas alumno
Textos Escolares Licitados por Mineduc

Grupo: Título del recurso

Unidades
Unidad 1: Números de más de 6 cifras. Cálculos con las cuatro operaciones y el uso de paréntesis. Reglas de secuencias numéricas. Ecuaciones.
Números naturales de más de seis cifras. Cálculos con las cuatro operaciones y el uso de paréntesis. Ecuaciones e inecuaciones de un paso. Secuencias numéricas.
Unidad 2: Localización y figuras 2D. Congruencia. Medición de longitudes. Áreas y perímetros de rectángulos, cuadrados, triángulos, paralelogramos y trapecios.
Localización en el plano cartesiano. Descripción de figuras 2D y 3D. Congruencia de figuras utilizando la traslaci+on, refelxión y rotación. Medir longitudes con unidades estandarizadas m, cm, mm. Transformación de unidades de medidas. Elaboración de rectángulos con condiciones para el área y el perímetro. Cálculo de áreas de figras 2D.
Unidad 3: Fracciones y números decimales. Adición y sustracción de fracciones propias.
Transformación de fraciones en números decimales y viceversa. Resolución de probleas que involucran la adición y la sustracción de fracciones con denominadores hasta 12 y números decimales hasta la milésima.
Unidad 4: Estadísticas y azar
Estadística: lectura e interpretación de tablas y gráficos (de barras y circulares). Azar: posibilidad de ocurrencia de un evento. Concepto de promedio aritmético.