57 horas pedagógicas
Unidad 3: Ángulos. Círculo. Área y de triángulos, paralelogramos y trapecios. Puntos en el plano.
Ángulos interiores y exteriores. Comprender el círculo. Construcción de líneas paralelas, perpendiculares y líneas especiales en el triángulo, cuadriláteros y círculos. Desarrollo de la fórmula del área de triángulos, paralelogramos y trapecios. Puntos y vectores en el plano cartesiano.
Propósito
En esta unidad, los estudiantes descubren relaciones entre la suma de ángulos interiores y exteriores de polígonos y conjeturan sobre el área de superficies de triángulos, paralelogramos y trapecios. Trabajan con el círculo y descubren de manera experimental la relación entre el diámetro y el perímetro, encontrando una estimación de pi (aproximadamente 3) por medio de mediciones concretas. Usan este nuevo conocimiento en la fórmula del área del círculo, en la resolución de problemas relacionados con geometría y en contexto con la construcción, el diseño y otros temas de la vida real. El conocimiento de pi se trata como constante en las fórmulas del perímetro y el área de un círculo. Los estudiantes comprenden que la circunferencia es un lugar geométrico, cuya característica radica en los puntos que están a igual distancia del centro; emplean este concepto para construir rectas perpendiculares, paralelas, puntos medios y bisectrices con regla y compás, y triángulos y cuadriláteros congruentes. También se incorpora la noción de vectores representados en el plano cartesiano por medio de juegos de posición; como usarán este concepto frecuentemente, el primer acercamiento debe ser progresivo y lúdico.
Conocimientos previos
- Construcción de triángulos.
- Área de superficie de cubos y paralelepípedos.
- Traslaciones, reflexiones y rotaciones.
- Ángulos agudos, obtusos, rectos extendidos y completos.
- Suma de los ángulos interiores de un triángulo.
- Suma de los ángulos interiores de un cuadrilátero.
Palabras claves
Suma de ángulos, polígonos, paralelogramos, trapecios, pi, perímetro del círculo, áreas de superficies, construcción, vectores.
Objetivos de la unidad
Descubrir relaciones que involucran ángulos exteriores o interiores de diferentes polígonos.
Indicadores
Indicadores Unidad 3
- Reconocen polígonos en las caras y en las secciones de poliedros y de prismas, en cruces de varillas, sombras, etc.
- Verbalizan reglas para obtener polígonos regulares.
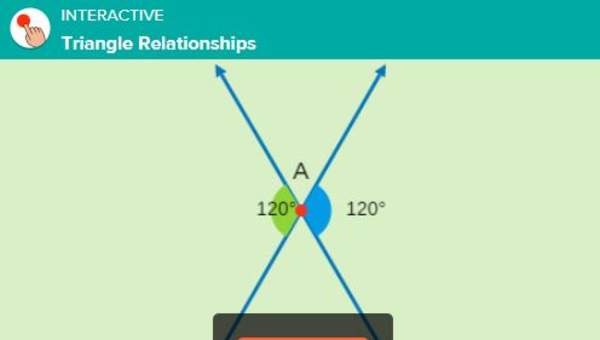
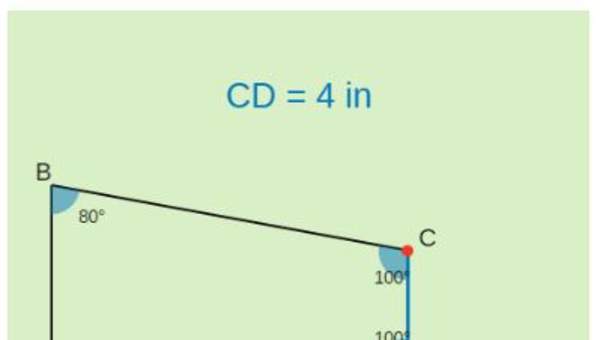
- Estiman la suma de los ángulos interiores en polígonos y verifican los resultados, midiéndolos.
- Muestran geométricamente, mediante la descomposición en triángulos, el patrón de la suma de los ángulos interiores en polígonos.
- Determinan la medida del ángulo del centro de un polígono regular para encontrar la medida del ángulo interior mediante la construcción de un triángulo.
- Aplican el concepto de ángulo interior de polígonos a situaciones concretas o pictóricas.
- Resuelven problemas geométricos, aplicando el patrón de la suma de ángulos interiores y exteriores.
Mostrar que comprenden el círculo:
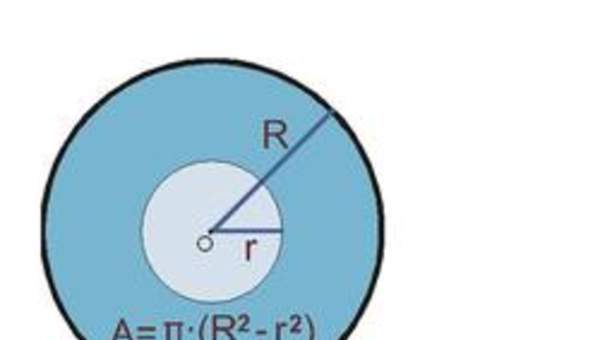
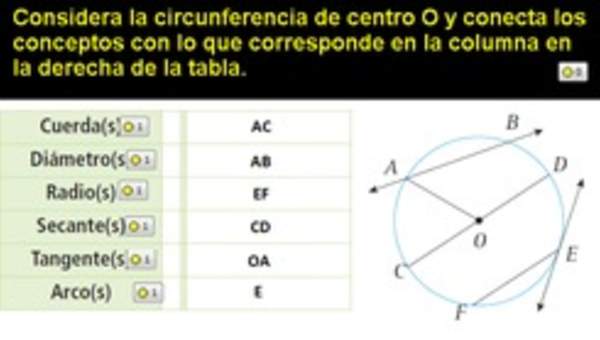
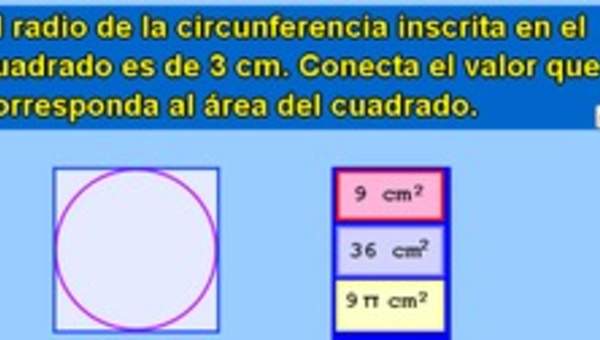
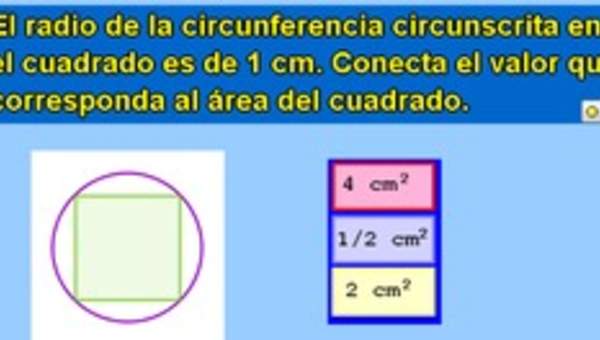
- Describiendo las relaciones entre el radio, el diámetro y el perímetro del círculo.
- Estimando de manera intuitiva el perímetro y el área de un círculo.
- Aplicando las aproximaciones del perímetro y del área en la resolución de problemas.
- Geométricos de otras asignaturas y de la vida diaria.
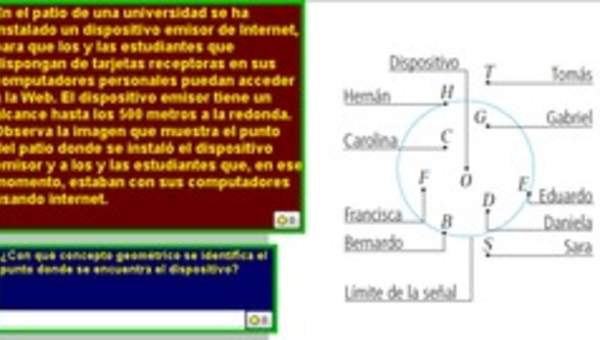
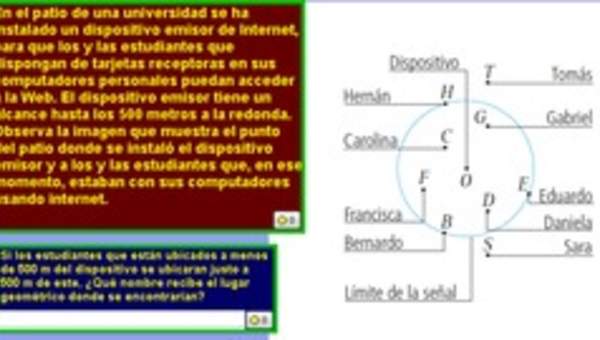
- Identificándolo como lugar geométrico.
Indicadores
Indicadores Unidad 3
- Identifican la línea del ecuador, paralelos y meridianos en modelos esféricos.
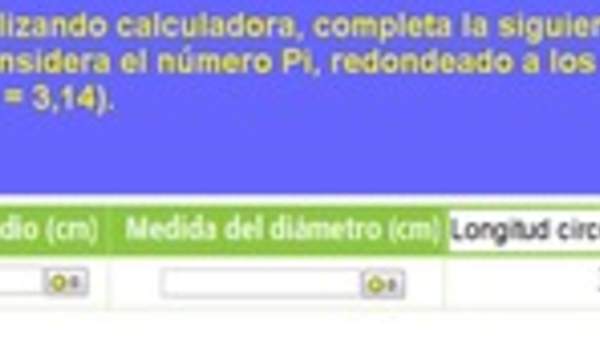
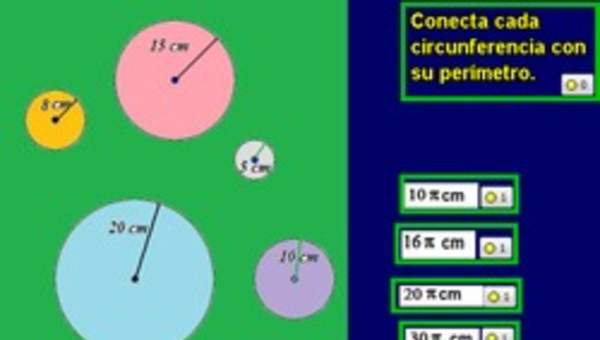
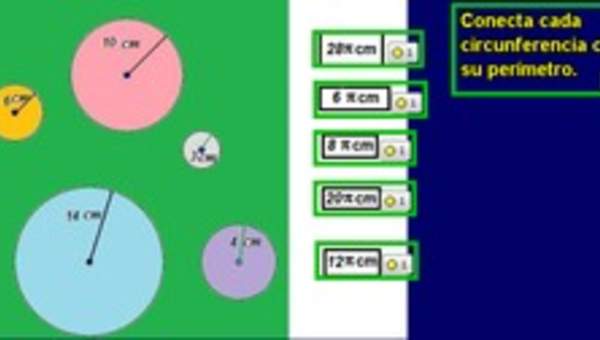
- Miden el diámetro y el perímetro de objetos redondos, como vasos con forma cilíndrica, latas, corchos, etc.
- Calculan el cociente entre el perímetro y el diámetro de una"pi" circunferencia y comparar el resultado con.
- Aplican la fórmula P = d t pi en ejercicios rutinarios y no rutinarios, para resolver problemas que involucran perímetros de círculos, como ecuador, paralelos y meridianos.
- Estiman el área del círculo entre 2r2 y 4r2, descubriendo que también resulta el mismo valor aproximado de a ≈ r 2 t 3.
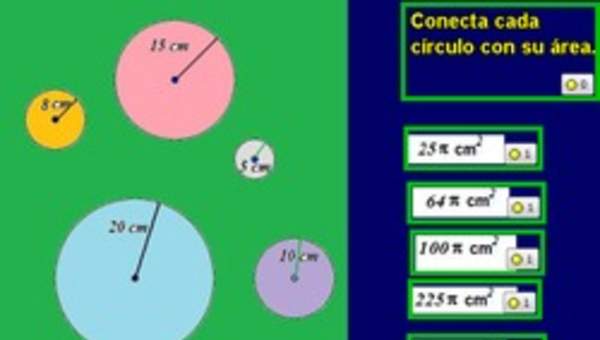
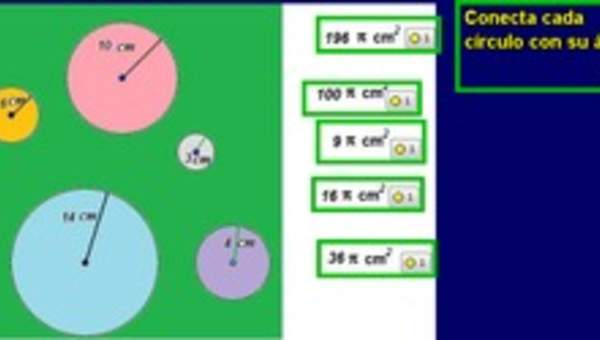
- Aplican la fórmula A = r2 t pi (con pi ≈3,14) en ejercicios rutinarios y en la solución de problemas que involucran áreas de círculos.
- Resuelven problema de la vida diaria que implican el cálculo de área de un círculo; por ejemplo: los cultivos en círculos para el ahorro de agua.
Construir objetos geométricos de manera manual y/o con software educativo:
- Líneas, como las perpendiculares, las paralelas, las bisectrices y alturas en triángulos y cuadriláteros.
- Puntos, como el punto medio de un segmento, el centro de gravedad, el centro del círculo inscrito y del circunscrito de un triángulo.
- Triángulos y cuadriláteros congruentes.
Indicadores
Indicadores Unidad 3
- Aplican la propiedad del círculo como lugar geométrico para resolver problemas concretos; por ejemplo: la cobertura de una radioemisora, etc.
- Construyen la recta perpendicular a un punto en una recta y reconocen que la recta perpendicular a un punto fuera de ella, tiene la distancia mínima entre el punto y la recta.
- Experimentan, concretamente o en forma pictórica, que doblando dos veces en dirección perpendicular, se continúa paralelamente a la dirección original, y aplican esto para construir paralelas de una recta.
- Construyen la altura en un triángulo isósceles, observando que lo divide en dos triángulos simétricos, y aplican este procedimiento para construir bisectrices.
- Aplican la construcción para resolver problemas de la vida diaria, mediante líneas perpendiculares, paralelas, bisectriz, triángulos y cuadriláteros.
Desarrollar y aplicar la fórmula del área de triángulos, paralelogramos y trapecios.
Indicadores
Indicadores Unidad 3
- Dibujan cuadriláteros a partir de un triángulo dado.
- Reconocen que el área de un triángulo se obtiene por dividir un cuadrilátero por una de sus diagonales.
- Transforman paralelogramos en rectángulos de la misma altura por medio de recortes o dibujos, reconociendo que se mantiene la medida del área.
- Formulan verbal y simbólicamente la regla para calcular el área de paralelogramos.
- Descomponen concreta o pictóricamente un paralelogramo en dos triángulos con el mismo contenido, verificando que el área de un triángulo se calcula como medio paralelogramo con la misma base y altura.
- Recortan o dibujan dos trapecios iguales y confeccionan o dibujan un paralelogramo con la misma altura y el doble del área, obteniendo la fórmula del área de un trapecio.
- Resuelven problemas geométricos y de la vida cotidiana, cuya resolución requiere calcular áreas de triángulos, paralelogramos y trapecios.
Identificar puntos en el plano cartesiano, usando pares ordenados y vectores de forma concreta (juegos) y pictórica.
Indicadores
Indicadores Unidad 3
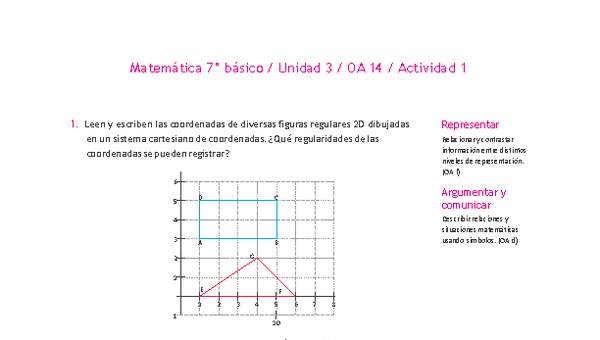
- Construyen segmentos y figuras en los cuatro cuadrantes del plano cartesiano, usando coordenadas enteras.
- Dibujan figuras 2D a partir de los pares de coordenadas dadas, y leen y comunican las coordenadas de figuras 2D dadas en el sistema de coordenadas.
- Conjeturan la forma y la ubicación de figuras 2D (rectángulo, cuadrado, paralelogramo y trapecio) a partir de los cuatro pares de coordenadas dadas, y las verifican pictóricamente.
- Dibujan figuras 2D y descubren que las formas se mantienen si se traslada el sistema, aunque las coordenadas se cambian.
Trabajar en equipo, en forma responsable y proactiva, ayudando a los otros, considerando y respetando los aportes de todos, y manifestando disposición a entender sus argumentos en las soluciones de los problemas.
Demostrar interés, esfuerzo, perseverancia y rigor frente a la resolución de problemas y la búsqueda de nuevas soluciones para problemas reales.
Demostrar curiosidad e interés por resolver desafíos matemáticos, con confianza en las propias capacidades, incluso cuando no se consigue un resultado inmediato.
Usar modelos, realizando cálculos, estimaciones y simulaciones, tanto manualmente como con ayuda de instrumentos para resolver problemas de otras asignaturas y de la vida diaria.
Utilizar sus propias palabras, gráficos y símbolos matemáticos para presentar sus ideas o soluciones.
Evaluar la argumentación de otros dando razones.
Describir relaciones y situaciones matemáticas de manera verbal y usando símbolos.
Explicar y fundamentar:
- Soluciones propias y los procedimientos utilizados.
- Resultados mediante definiciones, axiomas, propiedades y teoremas.
Fundamentar conjeturas dando ejemplos y contraejemplos.
Recursos de la unidad
Actividades evaluativas
Actividades evaluativas
Actividades evaluativas
Actividades evaluativas
Actividades complementarias
Actividades complementarias
Actividades complementarias
Actividades complementarias
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Actividades sugeridas
Lecciones
Lecciones
Lecciones
Lecciones
Lecciones
Lecciones
Lecciones
Lecciones
Imágenes
Imágenes
Imágenes
Imágenes
Imágenes
Imágenes
Imágenes
Imágenes
Imágenes
Imágenes
Imágenes
Imágenes
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Interactivos
Videos
Videos
Videos
Lecturas alumno
Textos Escolares Licitados por Mineduc
Textos Escolares Licitados por Mineduc
Textos Escolares Licitados por Mineduc
Textos Escolares Licitados por Mineduc
