48 horas pedagógicas
Unidad 3: Teorema de Pitágoras. Prismas y cilindros. Posición y movimientos.
Descubrir el teorema de Pitágoras y aplicarlo en la resolución de problemas. Cálculo del área de la superficie y del volumen de prismas y cilindros. Combinación de traslaciones, reflexiones y rotaciones.
Propósito
En esta unidad, los estudiantes descubren y aplican las fórmulas del área de superficies y del volumen de prismas rectos y de cilindros. Para ello, comienzan con cuerpos conocidos, como el cubo, y trabajan con sus redes para determinar las relaciones entre largo, ancho y alto, necesarias para desarrollar el nuevo conocimiento.
El foco de esta unidad está en el teorema de Pitágoras, que se introduce desde lo concreto de sus aplicaciones, con dibujos explicativos y con una demostración matemática, pero sencilla del mismo. Los alumnos deben resolver problemas que involucren dicho teorema en contextos como la geometría, la construcción y el arte.
Se recomienda integrar material concreto o algún medio tecnológico visual que les permita aprovechar al máximo la riqueza del teorema.
Otro foco radica en la descripción de movimientos como la traslación, la rotación y la reflexión. Los alumnos se pueden apoyar en el plano cartesiano y en las posibilidades que ofrece para este tema. Dentro de la descripción de movimientos, se comienza con algunos sencillos para continuar con la composición de dos o más de estos movimientos; la motivación puede provenir del arte o la matemática. También se sugiere usar aquí medios visuales o material concreto para ayudar a los estudiantes a desarrollar su capacidad espacial.
Conocimientos previos
- Operaciones con números racionales.
- Ecuaciones con soluciones racionales.
- Construcción de triángulos.
- Área de superficie de cubos y paralelepípedos.
- Traslaciones, reflexiones y rotaciones.
Palabras claves
Prismas rectos, cilindros, redes de cuerpos, teorema de Pitágoras, plano cartesiano, espacio, rotación, traslación, reflexión, composición de movimientos.
Objetivos de la unidad
Desarrollar las fórmulas para encontrar el área de superficies y el volumen de prismas rectos con diferentes bases y cilindros:
- Estimando de manera intuitiva área de superficie y volumen.
- Desplegando la red de prismas rectos para encontrar la fórmula del área de superficie aplicando las aproximaciones del perímetro y del área en la resolución de problemas.
- Aplicando las aproximaciones del perímetro y del área en la resolución de problemas.
- Aplicando las fórmulas a la resolución de problemas geométricos y de la vida diaria.
Indicadores
Indicadores Unidad 3
- Arman y despliegan cajas de forma de prismas rectos.
- Reconocen que las áreas laterales de todos los prismas rectos son rectángulos.
- Elaboran redes de prismas rectos de diferentes bases y calculan las áreas de las superficies.
- Resuelven problemas cotidianos que involucran el volumen y el área de prismas rectos.
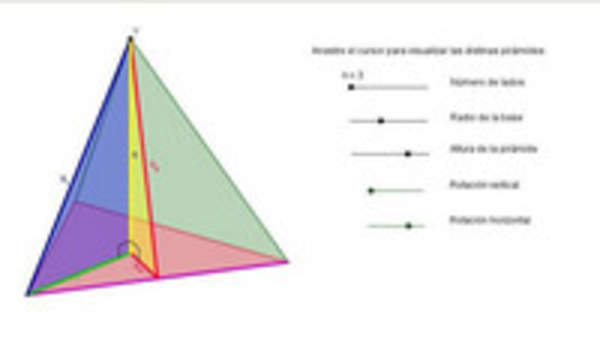
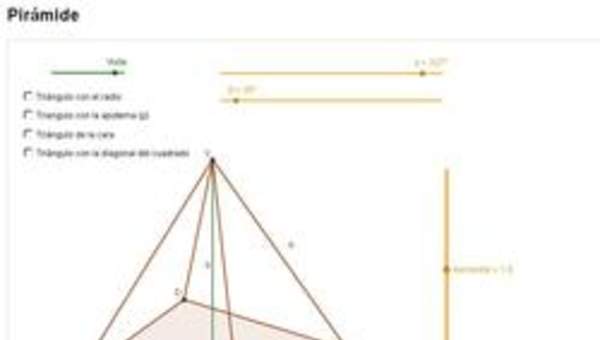
- Reconocen en forma intuitiva que los prismas a base de polígonos regulares se acercan a cilindros si se aumenta el número de los lados del prisma.
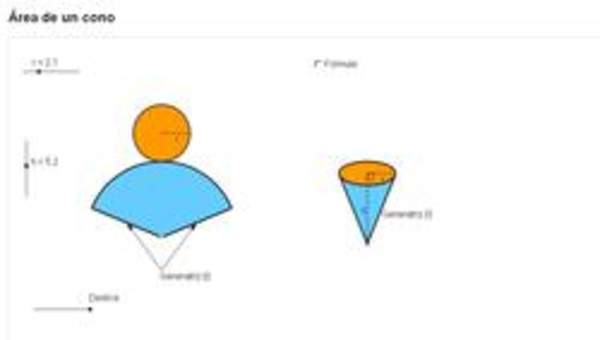
- Confeccionan de manera concreta modelos de cilindros y los comparan con modelos o dibujos de prismas a base de polígonos regulares.
- Transfieren la fórmula del volumen de un cubo para determinar la fórmula del volumen de un cilindro.
- Calculan el área de cilindros en ejercicios rutinarios.
- Resuelven problemas cotidianos y de ciencias relacionados con el área de la superficie y el volumen de cilindros.
Indicadores
Indicadores Unidad 3
- Descubren el teorema de Pitágoras concreta o pictóricamente, mediante descomposición o composición de cuadrados y triángulos rectángulos.
- Dibujan triángulos rectángulos con los cuadrados respectivos encima los catetos y la hipotenusa, y verifican la validez del teorema de Pitágoras.
- Reconocen que con dos lados del triángulo rectángulo dados, se puede calcular el tercer lado.
- Despejan algebraicamente la fórmula c2 = a 2 + b2 para cualquier variable.
- Estiman o calculan correctamente con la calculadora, las raíces cuadradas que resultan al aplicar el teorema de Pitágoras.
- Verifican con las medidas dadas de un triángulo si es rectángulo o no.
- Calculan el largo del lado faltante para que un triángulo sea rectángulo y lo verifican por construcción, aplicando el teorema de Tales (triángu inscritos en una semicircunferencia).
- Calculan los componentes perpendiculares de vectores dados.
- Resuelven problemas cotidianos para calcular el largo de lados desconocidos y no accesibles en el plano y en el espacio, determinando primero los triángulos rectángulos respectivos.
Describir la posición y el movimiento (traslaciones, rotaciones y reflexiones) de figuras 2D, de manera manual y/o con software educativo, utilizando:
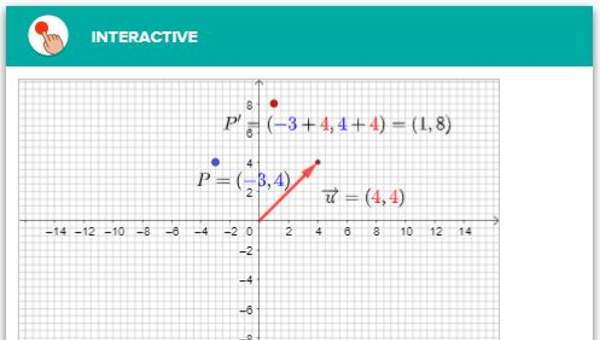
- Los vectores para la traslación.
- Los ejes del plano cartesiano como ejes de reflexión.
- Los puntos del plano para las rotaciones.
Indicadores
Indicadores Unidad 3
- Realizan traslaciones en el plano con vectores dados.
- Determinan el vector entre la imagen y la pre- imagen de 2 figuras 2D trasladadas y modelan la traslación y la combinación de traslaciones, por medio de vectores y la suma de ellos.
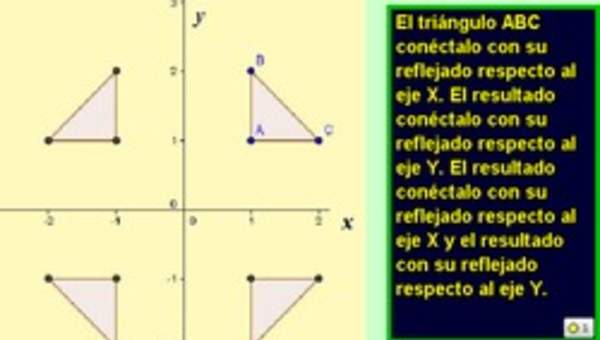
- Reflexionan figuras 2D según los ejes dados, de manera concreta y pictórica.
- Determinan el eje de reflexión entre la imagen y la pre-imagen de dos figuras 2D.
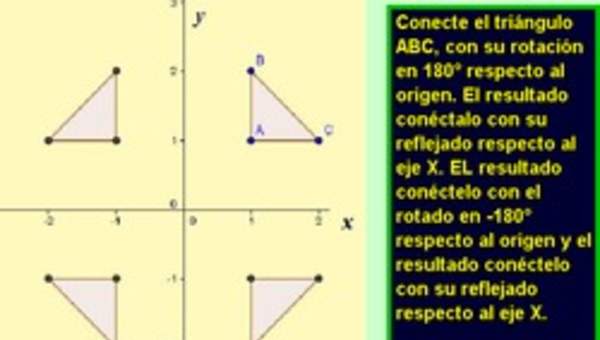
- Reconocen que la rotación por 180° es una reflexión en un punto, llamado punto de simetría.
- Identifican rotaciones, reflexiones y traslaciones en situaciones cotidianas.
Indicadores
Indicadores Unidad 3
- Realizan diferentes combinaciones de traslaciones, reflexiones y rotaciones y reconocen las propiedades.
- Realizan teselados con figuras 2D, según los patrones dados.
- Identifican patrones de teselados dados, descubriendo experimentalmente las propiedades de la congruencia; es decir, la conservación de la medida de segmentos y de ángulos.
- Reconocen transformaciones isométricas dadas en el plano, identificando puntos importantes, como vector de traslación, centro de rotación, ángulo de rotación, eje o punto de reflexión.
Explicar y fundamentar:
- Soluciones propias y los procedimientos utilizados.
- Resultados mediante definiciones, axiomas, propiedades y teoremas.
Recursos de la unidad
Actividades evaluativas
Actividades complementarias
Actividades sugeridas
Lecciones
Audios
Imágenes
Interactivos
Presentaciones
Simulaciones
Videos
Lecturas alumno
Textos Escolares Licitados por Mineduc

Grupo: Título del recurso

Unidades
Unidad 1: Raices cuadradas. Multiplicación y división de números enteros y de potencias.
Los alumnos toman primer contacto con raices cuadradas verificando que elevar al cuadrado y sacar la raíz cuadrada son operaciones inversas.
Unidad 2: Expresiones algebraicas. Noción de función. Cambio lineal y afín. Ecuaciones e inecuaciones lineales.
Operaciones con expresiones algebraicas. Primer contacto con la noción de función mediante el cambio lineal y afín. Aplicación de las propiedades de la función afín en la resolución de problemas de la vida diaria. Modelamiento con ecuaciones e inecuaciones lineales.
Unidad 3: Teorema de Pitágoras. Prismas y cilindros. Posición y movimientos.
Descubrir el teorema de Pitágoras y aplicarlo en la resolución de problemas. Cálculo del área de la superficie y del volumen de prismas y cilindros. Combinación de traslaciones, reflexiones y rotaciones.
Unidad 4: Medidas de posición y el principio combinatorio multiplicativo de probabilidades
Trabajo con medidas de posición -cuartiles y percentiles- y diagramas de cajón. Introducción del principio combinatorio multiplicativo de probabilidades.